
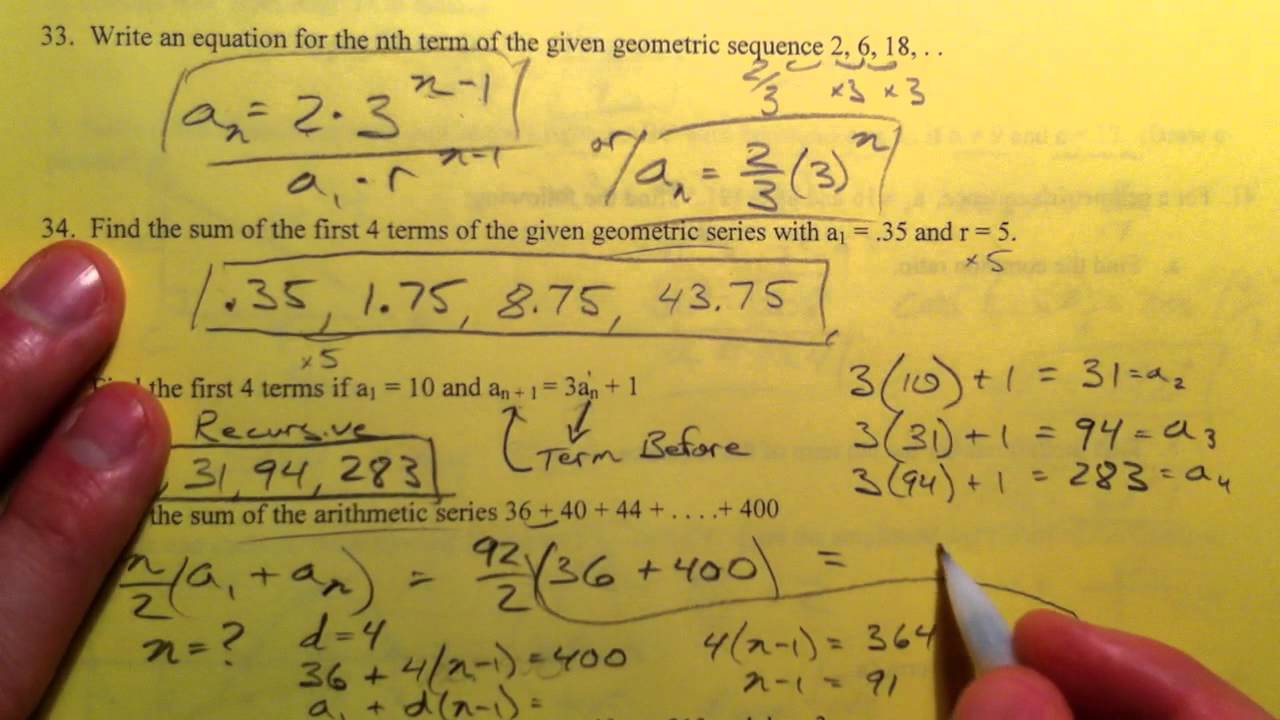
x 2 ( c 2 − a 2 ) − a 2 y 2 = a 2 ( c 2 − a 2 ) Factor common terms. c 2 x 2 − a 2 x 2 − a 2 y 2 = a 2 c 2 − a 4 Rearrange terms. a 4 + c 2 x 2 = a 2 x 2 + a 2 c 2 + a 2 y 2 Combine like terms. c 2 x 2 − 2 a 2 c x + a 4 = a 2 x 2 − 2 a 2 c x + a 2 c 2 + a 2 y 2 Distribute a 2. c 2 x 2 − 2 a 2 c x + a 4 = a 2 ( x 2 − 2 c x + c 2 + y 2 ) Expand the squares. ( c x − a 2 ) 2 = a 2 ( ( x − c ) 2 + y 2 ) 2 Square both sides. c x − a 2 = a ( x − c ) 2 + y 2 Divide by 4.


4 c x − 4 a 2 = 4 a ( x − c ) 2 + y 2 Isolate the radical. 2 c x = 4 a 2 + 4 a ( x − c ) 2 + y 2 − 2 c x Combine like terms.

x 2 + 2 c x + c 2 + y 2 = 4 a 2 + 4 a ( x − c ) 2 + y 2 + x 2 − 2 c x + c 2 + y 2 Expand remaining square. x 2 + 2 c x + c 2 + y 2 = 4 a 2 + 4 a ( x − c ) 2 + y 2 + ( x − c ) 2 + y 2 Expand the squares. ( x + c ) 2 + y 2 = ( 2 a + ( x − c ) 2 + y 2 ) 2 Square both sides. ( x + c ) 2 + y 2 = 2 a + ( x − c ) 2 + y 2 Move radical to opposite side. See Figure 3.ĭ 2 − d 1 = ( x − ( − c ) ) 2 + ( y − 0 ) 2 − ( x − c ) 2 + ( y − 0 ) 2 = 2 a Distance Formula ( x + c ) 2 + y 2 − ( x − c ) 2 + y 2 = 2 a Simplify expressions. To sketch the asymptotes of the hyperbola, simply sketch and extend the diagonals of the central rectangle. The central rectangle of the hyperbola is centered at the origin with sides that pass through each vertex and co-vertex it is a useful tool for graphing the hyperbola and its asymptotes. As a hyperbola recedes from the center, its branches approach these asymptotes. Every hyperbola also has two asymptotes that pass through its center. The center of a hyperbola is the midpoint of both the transverse and conjugate axes, where they intersect. The conjugate axis is perpendicular to the transverse axis and has the co-vertices as its endpoints. The foci lie on the line that contains the transverse axis. The transverse axis is a line segment that passes through the center of the hyperbola and has vertices as its endpoints. The distinction is that the hyperbola is defined in terms of the difference of two distances, whereas the ellipse is defined in terms of the sum of two distances.Īs with the ellipse, every hyperbola has two axes of symmetry. Notice that the definition of a hyperbola is very similar to that of an ellipse. A hyperbola is the set of all points ( x, y ) ( x, y ) in a plane such that the difference of the distances between ( x, y ) ( x, y ) and the foci is a positive constant. Like the ellipse, the hyperbola can also be defined as a set of points in the coordinate plane. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. We recommend using aĪuthors: Lynn Marecek, Andrea Honeycutt Mathis Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the In each term, the number of times a 1 a 1 is multiplied by r is one less than the number of the term. r or r 3 r 3) and in the fifth term, the a 1 a 1 is multiplied by r four times.In the fourth term, the a 1 a 1 is multiplied by r three times ( r In the third term, the a 1 a 1 is multiplied by r two times ( r In the second term, the a 1 a 1 is multiplied by r. The first term, a 1, a 1, is not multiplied by any r. We will then look for a pattern.Īs we look for a pattern in the five terms above, we see that each of the terms starts with a 1. Let’s write the first few terms of the sequence where the first term is a 1 a 1 and the common ratio is r. Just as we found a formula for the general term of a sequence and an arithmetic sequence, we can also find a formula for the general term of a geometric sequence. Find the General Term ( nth Term) of a Geometric Sequence Write the first five terms of the sequence where the first term is 6 and the common ratio is r = −4.


 0 kommentar(er)
0 kommentar(er)
